Ejemplo
Un rotor de un motor eléctrico que tiene un momento de inercia $J$, conformado de diferentes materiales (heterogéneo) y está montado sobre cojinetes que aplican una fricción viscosa $b$ al eje del rotor. Suponga que no se le aplica una fuerza externa al rotor y que el único par que actúa sobre él, es la velocidad angular $w(0)=w_{0}$ y la fricción $b$ debida a los cojinetes. Determine como se comportará la velocidad angular $w$.
Figura 1: Rotor con momento de inercia $J$ sobre dos cojinetes, con fricción viscosa $b$.
La Figura 1 muestra el rotor montado sobre los cojinetes que gira a una velocidad angular $\dot{\theta}=w$. Por lo tanto la velocidad angular inicial es de $w(0)=w_{0}$. Con esto es posible determinar la ecuación de movimiento.
\begin{equation}
J \ddot{\theta}+b\dot{theta}=0
\label{ectheta}
\end{equation}
La ecuación de movimiento mostrada en \ref{ectheta} también puede ser vista en función de la velocidad angular $w$ en vez de ser vista desde el movimiento del ángulo $\theta$, quedando,
\begin{equation}
J \dot{w}+bw=0
\label{ecw}
\end{equation}
La ecuación diferencial \ref{ecw} es de primer orden y a los sistemas descritos por una ecuación de este tipo se les conoce como sistemas de primer orden.
Para resolver este sistema, utilice la forma exponencial vista en la sección Análisis de sistemas dinámicos,
\begin{equation}
w=w_{0}e^{\lambda t}
\label{exp1}
\end{equation}
derivando la ecuación \ref{exp1} con respecto al tiempo $t$ se obtiene,
\begin{equation}
\dot{w}=w_{0} \lambda e^{\lambda t}.
\label{exp2}
\end{equation}
La ecuación \ref{exp1} y \ref{exp2} se sustituyen en \ref{ecw},
\begin{equation}
J w_{0} \lambda e^{\lambda t}+b w_{0}e^{\lambda t}=0.
\label{solw}
\end{equation}
Factorizando términos, se obtiene,
\begin{equation}
w_{0} e^{\lambda t}(J \lambda +b )=0,
\label{solw2}
\end{equation}
note que la ecuación \ref{solw2} solo puede hacerse cero si,
\begin{equation}
J \lambda +b=0,
\label{ecar}
\end{equation}
debido a que $w_{0} e^{\lambda t} \neq 0$. A la ecuación \ref{ecar} se le conoce como la ecuación característica del sistema, se le conoce de esta forma porque depende de las características intrínsecas del sistema, de la cantidad de masa, es decir su momento de inercia $J$ y el tipo de viscosidad $b$ del sistema, estas características determinan el valor de
\begin{equation}
\lambda =-\frac{b}{J}.
\label{lamda}
\end{equation}
Sustituyendo $\lambda$ en \ref{exp1} se obtiene la respuesta del sistema de acuerdo a sus características, es decir,
\begin{equation}
w=w_{0}e^{-\frac{b}{J} t}.
\label{resp1}
\end{equation}
Lo que indica que la respuesta del sistema, es decir el comportamiento de la velocidad angular $w$ cuando tiene una velocidad angular inicial $w_{0}$ y las características de momento de inercia $J$ y viscosidad $b$.
Para conocer como se comporta la velocidad se necesita sustituir los valores de $w_{0}$, $J$ y $b$. Además se debe observar el comportamiento del sistema por un tiempo $t$ y apuntar la velocidad angular cada cierto tiempo para poder graficarla. Para evitar hacer esto a mano, se utilizará el programa de Matlab para simular y graficar el comportamiento de este sistema.
A continuación se anexa el programa de Matlab que sirve para realizar la simulación de la respuesta \ref{resp1} del sistema \ref{ecw}.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Programa que sirve para obtener la gráfica de la respuesta % % del movimiento inercial de un rotor con cojinetes y fricción % % viscosa. % % Hecho por: Dr. Raúl Dalí Cruz Morales % % % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clc %Limpia la pantalla de comandos y respuestas previas clear all %Limpia las variables guardadas en el workspace. %% Declaración de variables y condiciones iniciales. % del sistema w(t)=w(0)e^(-(b/j)t) w0=6; %Condiciones inicial de w(0) b=2.5; %Fricción viscosa j=8; %Inercia t=0:0.1:10; % crea un vector de tiempo de simulación de 0 a 10 s % con incrementos de 0.1 s %% Procesamiento de datos w=w0*exp(-(b/j)*t); %Respuesta del sistema %% Gráfica de respuesta del sistema. plot(t,w,'LineWidth',2) %Grafica el tiempo vs vel. angular en (x,y) respectivamente xlabel('Tiempo (s)') %Coloca la leyenda 'Tiempo (s)' en el eje X ylabel('Velocidad (rad/s)') %Coloca la leyenda 'Velocidad (rad/s)' en el eje Y title('Respuesta w(t)=w_{0}*e^{-(b/j)*t}') % Coloca título a la gráfica. |
De este programa se obtiene la siguiente gráfica,
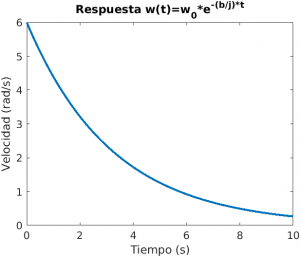Figura 2. Gráfica obtenida en matlab, velocidad vs tiempo.
En la Fígura 2, se observa que la velocidad inicial del rotor es de 6 $rad/s$ en el tiempo $t=0$, y conforme el tiempo avanza, la velocidad de rotación va disminuyendo exponencialmente, esto es acorde a la ecuación \ref{resp1}, nótese que en el tiempo $t=10 s$ el rotor está casi detenido. Si la simulación se hace por más tiempo, se podrá observar el tiempo que tarda en detenerse completamente el rotor.
Con esto se puede analizar el comportamiento del robot, y simular su movimiento y el tiempo que tardará en detenerse de acuerdo a la velocidad inicial y las características intrínsecas del sistema.