Control PID – Dinámica de sistemas físicos

Para entender mejor el funcionamiento del control PID. Se debe recordar que un sistema puede estar en lazo abierto o en lazo cerrado.

Un sistema en lazo abierto puede ser como cuando se enciende una motor para una bomba hidráulica y esta sube agua a un tinaco hasta que alguien apague el motor.

Figura1: Diagrama a bloques de un sistema en lazo abierto

La Figura 1 muestra el diagrama a bloques de el sistema mencionado, F(s) es la entrada (interruptor), $T_{1}(s)$ es el motor y la salida $X(s)$ es el agua que sube al tinaco, este sistema seguirá funcionando hasta que la misma persona que encendió la bomba, regrese y la apague.

Si a este mismo sistema le añadimos un sensor que pueda detectar cuando el tinaco se ha llenado y mande una señal indicando que está lleno para apagar la bomba, entonces el sistema está siendo controlado en lazo cerrado y se conoce como un control en lazo cerrado.

Figura 2: Diagrama a bloques de un sistema en lazo cerrado

En la Figura 2 el sensor es representado por $H(s)$ y su señal por $D(s)$, esta señal es comparada con una señal de referencia dada en la entrada y se restan, al ser iguales entonces el sistema ha llegado a la referencia o al punto deseado, y en este caso se podría detener la bomba hasta que el agua baje de cierto nivel de referencia y tenga que ser encendida de nuevo.

Una vez que se recordó esto, al tener una función de transferencia de un sistema dinámico, se le puede aplicar un control del tipo PID (proporcional, integral y derivativo).

Cada una de estas tres palabras, definen algo que hace el control.

Proporcional: La ganancia proporcional en un control PID ayuda a reducir el error en estado estable, entre la señal de referencia y la señal de control. Si se usa solo, el error en estado estable se mantiene.
Integral: La ganancia integral, ayuda a reducir el error constante que queda al usar solo la ganancia proporcional, esta ganancia genera una señal de control que es proporcional a la integral del error. Puede generar inestabilidad al sistema y oscilaciones.
Derivativo: La ganancia derivativa, ayuda a reducir las oscilaciones generadas por el control integral, ya que reacciona a la velocidad e cambio del error y la señal de control depende de la derivada del error. Reduce las oscilaciones, mejora el tiempo de respuesta pero incrementa el ruido en las señales de medición.

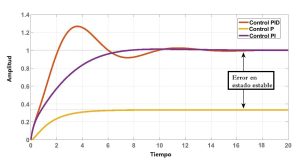Figura 3: Respuesta de un sistema al control P, PI y PID

Juntos forman el Control Proporcional-Integral-Derivativo mejor conocido como control PID. Y sirve para que la señal de control rápidamente llegue a la señal de referencia deseada.

Simulación de un control PID con Matlab.

Al hacer uso del software Matlab, se puede simular el comportamiento de cualquier sistema al que se le aplique un control PID.

La forma mas directa de realizar la simulación, es teniendo la función de transferencia del sistema, por ejemplo si se tiene un sistema de la forma

\begin{equation}
\ddot{x}+5\dot{x}+2=u(t)
\label{S1}
\end{equation}

entonces se puede utilizar el comando $tf$ en matlab para obtener la función de transferencia, de la forma,

\begin{equation}
ND=tf(1, [1 \ \ 5 \ \ 2])
\label{ND}
\end{equation}

y se obtiene la función de transferencia del sistema \ref{S1} que será guardada en la variable $ND$. Además para cerrar el lazo de esta función de transferencia \ref{ND} se obtiene utilizando la función $feedback$ de la siguiente manera,
\begin{equation}
SN=feedback(ND,1)
\label{FB}
\end{equation}

Donde el sistema resultante se guarda en $SN$, a este sistema \ref{FB} se le puede aplicar una entrada del tipo escalón unitario para analizar la respuesta que tendrá, esto se realiza al utilizar la función $step$,
\begin{equation}
step(SN)
\label{SN}
\end{equation}
y matlab genera automáticamente una gráfica de la respuesta de este sistema. En este caso la señal de referencia es 1 y por lo tanto el sistema debería quedar estable en 1. Al no tener control, la señal puede que no llegue a la referencia de 1 y quede con un error en estado estacionario.

Para reducir o anular ese error, se debe realizar un control PID, para esto se debe definir el valor de las constantes proporcional, integral y derivativa del control y después utilizar el comando
\begin{equation}
CR=pid(kp,ki,kd)
\label{kpid}
\end{equation}
generando un control PID de la forma,
\begin{equation}
CR=kp+\frac{ki}{s}+kd*s
\label{cpid}
\end{equation}
Con este control \ref{kpid} y el sistema \ref{ND} se puede cerrar el lazo nuevamente y obtener el sistema en lazo cerrado con el controlador PID, de la forma,
\begin{equation}
RG=feedback(CR*ND,1)
\label{RG}
\end{equation}
y aplicar una entrada de tipo escalón para obtener la respuesta del sistema. Con lo cual se obtiene lo siguiente,

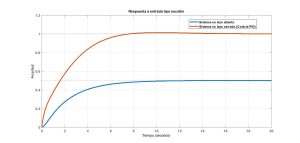Figura 4: Respuesta de un sistema sin control y con control PID

En la figura 4 se muestra la respuesta de un sistema en lazo abierto (azul) y se nota que no llega a la referencia que es 1, su error en estado estacionario es de 0.5, por otro lado, el sistema en lazo cerrado (naranja) y con control PID llega correctamente a la referencia de 1.

A continuación se presenta el programa en Matlab para generar estos gráficos y entender mejor el comportamiento de un control PID, se motiva al lector a cambiar los parámetros $kp,ki,kd$ dentro del programa para observar el comportamiento de cada uno y como afecta la respuesta del sistema. También se puede colocar cualquier función de transferencia y obtener la gráfica de su respuesta, el programa está comentado para su mejor entendimiento.

El script para graficar este sistema o cualquier otro se muestra a continuación, solo es necesario adecuar los valores de la función de transferencia y de las constantes del control PID.

 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 % Este programa muestra el funcionamiento de un controlador   %
 % PID.                                                        %
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 clc        %Comando que limpia la command window
 clear all  %Comando que limpia el workspace de variables
 close all  %Comando que cierra cualquier gráfico abierto anteriormente

 
 %% Declaración de la función de transferencia y condiciones iniciales.
 % función de transferencia = 1 / ( s^2+5s+2)
 m=1; %valor que multiplica a s^2
 b=5; %valor que multiplica a s
 k=2; %valor final.
 %En caso de ser de mayor grado, se anexan tantas como sea el grado más el
 %valor final.
 
 ND=tf(1, [m b k]) %El comando "tf" genera la función de transferencia donde
                   %el 1 es el numerador y [m b k] es el denominador de 
                   %la función detransferencia
  
 step(ND) %El comando step genera una entrada tipo escalón unitario 
          %para la función guardada en ND.
 hold on  %Mantiene la gráfica en la ventana hasta que se ponga 
          %el comando hold off
 %% Declaración de las constantes P, I, D, para el control PID.
 
 kp=2; %Valor de la constante proporcional del control PID.
 ki=1; %Valor de la constante integral del control PID.
 kd=1; %Valor de la constante derivativa del control PID.
  
 CR=pid(kp,ki,kd) %El comado "pid" crea un controlador PID de la forma:
                  % CR= kp+ (ki/s) + kd*s
 
 RG=feedback(CR*ND,1) %Crea el lazo cerrado de la función ND con el 
                      % controlador CR 

 step(RG)
 grid on  %Activa la cuadrícula de fondo en la figura.
%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Este programa muestra el funcionamiento de un controlador %

% PID. %

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clc %Comando que limpia la command window

clear all %Comando que limpia el workspace de variables

close all %Comando que cierra cualquier gráfico abierto anteriormente

%% Declaración de la función de transferencia y condiciones iniciales.

% función de transferencia = 1 / ( s^2+5s+2)

m=1; %valor que multiplica a s^2

b=5; %valor que multiplica a s

k=2; %valor final.

%En caso de ser de mayor grado, se anexan tantas como sea el grado más el

%valor final.

ND=tf(1, [m b k]) %El comando "tf" genera la función de transferencia donde

%el 1 es el numerador y [m b k] es el denominador de

%la función detransferencia

step(ND) %El comando step genera una entrada tipo escalón unitario

%para la función guardada en ND.

hold on %Mantiene la gráfica en la ventana hasta que se ponga

%el comando hold off

%% Declaración de las constantes P, I, D, para el control PID.

kp=2; %Valor de la constante proporcional del control PID.

ki=1; %Valor de la constante integral del control PID.

kd=1; %Valor de la constante derivativa del control PID.

CR=pid(kp,ki,kd) %El comado "pid" crea un controlador PID de la forma:

% CR= kp+ (ki/s) + kd*s

RG=feedback(CR*ND,1) %Crea el lazo cerrado de la función ND con el

% controlador CR

step(RG)

grid on %Activa la cuadrícula de fondo en la figura.